| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- IT인프라
- 파이썬
- 데이터분석가
- 딥러닝
- 데이터분석
- 짧은생각
- 아키텍처
- 교육
- 자기개발
- 정보화
- 데이터
- 미니프로젝트
- 데이터다루기
- KT에이블스쿨5기
- DX컨설턴트
- 파이썬기초
- 머신러닝
- deeplearning
- KT에이블스쿨
- 데이터분석기초
- 인프라
- 구조
- 데이터다듬기
- 오답노트
- It
- 프로젝트
- MachineLearning
- 판다스
- 넘파이
- 데이터프레임
- Today
- Total
꾸준히 성장하기
[D+26] 교육 | 이변량 분석의 핵심: 수치-범주 & 범주-범주 간 관계 본문
안녕하세요, 여러분. 오늘은 데이터 분석의 핵심 주제 중 하나인 이변량 분석에서 매우 중요한 두 가지 유형의 관계에 대해 이야기하고자 합니다.
바로 수치와 범주 간의 관계, 그리고 범주와 범주 간의 관계입니다.
이 두 관계를 깊이 이해하는 것은 여러분이 DX 컨설턴트로서 역량을 키우는 데 크게 기여할 것입니다.
1. 수치(x)→범주(y) 간의 관계
1) 시각화: KDE Plot, Histogram
KDE Plot은 데이터의 분포를 부드럽게 표현해 주며, 특정 수치가 어떤 범주에 얼마나 자주 나타나는지 시각적으로 파악할 수 있게 합니다.
Histogram을 통해 각 범주 내의 수치 데이터의 분포를 별도로 확인할 수 있습니다. 이는 범주별로 수치 데이터가 어떻게 분포하는지를 이해하는 데 도움을 줍니다.
각각의 그래프는 가로선과 멀리 떨어질수록 대립가설(내 주장)이 타당해집니다.
수치 → 범주 이변량 분석 함수 코드
def eda_2_nc(data, feature, target):
plt.figure(figsize=(6, 10))
plt.subplot(3, 1, 1)
sns.kdeplot(x=feature, data=data, hue=target, common_norm=False)
plt.xlim(data[feature].min(), data[feature].max())
plt.grid()
plt.subplot(3, 1, 2)
sns.kdeplot(x=feature, data=data, hue=target, multiple='fill')
plt.axhline(data[target].mean(), color='r')
plt.xlim(data[feature].min(), data[feature].max())
plt.grid()
plt.subplot(3, 1, 3)
sns.histplot(x=feature, data=data, bins=30, hue=target, multiple='fill')
plt.axhline(data[target].mean(), color='r')
plt.xlim(data[feature].min(), data[feature].max())
plt.grid()
plt.show()
Age(나이) → Satisfaction(만족) 산점도
target = 'satisfaction'
feature = 'Age'
eda_2_nc(data, feature, target)
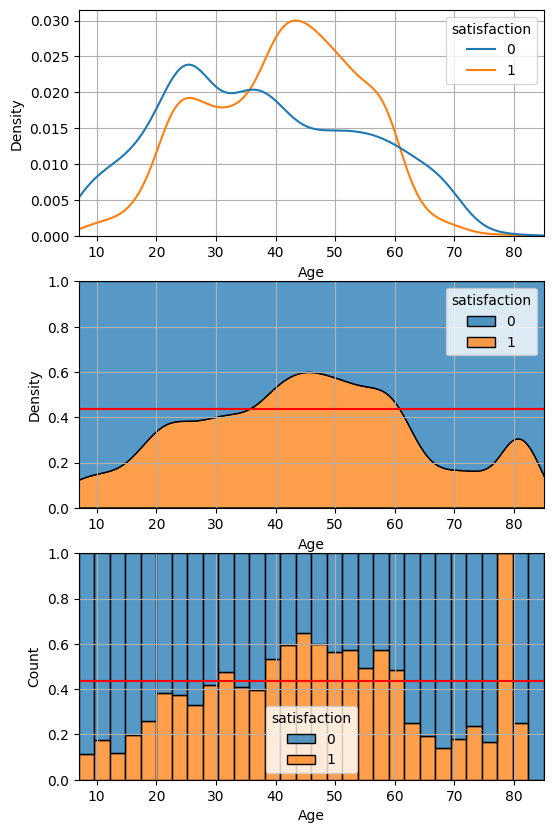
2) 수치화: -
수치와 범주 간의 관계에서는 일반적으 가설검증 방법을 직접 적용하기 어렵습니다.
하지만, 우리는 수치 데이터를 범주형 데이터로 변환하여 범주-범주 간의 관계로 다루거나,
수치 데이터를 가지고 범주-수치 관계로 접근하여 t-test나 ANOVA 같은 통계적 방법을 사용할 수 있습니다.
중요한 것은 분석하고자 하는 x와 y 사이에 선후관계가 설정되어서는 안 된다는 점입니다.
2. 범주(x)→범주(y) 간의 관계 "기대빈도로부터의 차"
1) 시각화: Mosaic Plot (모자익 플롯)
Mosaic Plot은 범주-범주 간의 관계를 시각화하는 데 유용한 도구입니다.
각 칸의 크기가 해당 범주 조합의 빈도를 나타내며, 이를 통해 변수 간의 관계를 직관적으로 이해할 수 있습니다.
Mosaic Plot을 사용할 때는 데이터의 정규화가 필요할 수 있습니다.
범주 → 범주 이변량 분석 함수 코드
mosaic(titanic, ['Sex', 'Survived'])
plt.axhline(1 - titanic['Survived'].mean(), color='r')
plt.show()
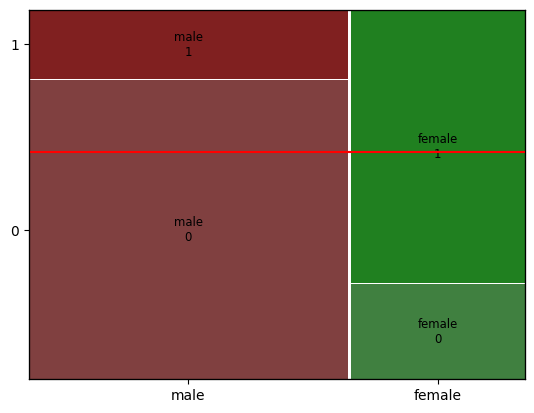
2) 수치화: 카이제곱 검정
두 범주형 변수 간의 독립성을 검정하는 통계적 방법입니다.
관측된 빈도와 기대된 빈도 간의 차이를 기반으로 하며, 이 차이가 클수록 우리는 두 변수 간에 유의미한 관계가 있다고 볼 수 있습니다.
범주 → 범주
pd.crosstab(titanic['Survived'], titanic['Sex'], normalize='all')
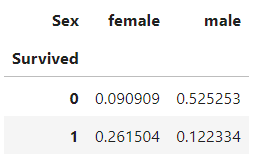
table = pd.crosstab(titanic['Survived'], titanic['Sex'])
print(table)
print('-' * 50)
spst.chi2_contingency(table)

이변량 분석에서 수치-범주 및 범주-범주 간의 관계를 이해하는 것은 여러분이 데이터를 통해 이야기를 발견하고 해석하는 데 필수적인 기술입니다.
오늘 공유한 내용이 여러분의 데이터 분석 여정에 도움이 되길 바랍니다. 데이터와 함께하는 여정에서 항상 새로운 발견이 있기를 기대합니다.
'KT 에이블스쿨 5기 > 교육' 카테고리의 다른 글
| [D+34] 교육 | 데이터 분석 표현, Streamlit (0) | 2024.03.25 |
|---|---|
| [D+27] 교육 | 데이터 크롤링의 기본과 접근 방법(정적 페이지 크롤링) (0) | 2024.03.18 |
| [D+24] 교육 | 이변량 분석의 핵심: 수치-수치 & 범주-수치 간 관계 (0) | 2024.03.15 |
| [D+22] 교육 | 개별 변수 분석, 단변량 분석 (0) | 2024.03.13 |
| [D+21] 교육 | 범주형 자료와 수치형 자료 (1) | 2024.03.12 |




